Archimedes poised to measure a circle behind him in the distance.
Posted on by Jason Cox

A Slice of Pi

Circles. Those fascinating geometric shapes have perplexed us for millennia. The Babylonians began poking at these mysterious objects 4,000 years ago and discovered that the distance around a circle was slightly greater than 3 times its width, specifically 3 1/8 or 3.125, which they recorded on a stone tablet. About the same time, Egyptians, seeking the area of a circle, estimated the ratio to be 3.1605 and recorded their estimation in the Rhind Papyrus (1650 BC).

Fast forward to ancient Greece, Antiphon and Bryson of Heraclea developed the innovative idea of inscribing a polygon inside a circle, finding its area, and doubling the sides over and over. Unfortunately, their approach meant finding the areas of hundreds of tiny triangles, which was complicated and yielded very little results. Then came Archimedes. Instead of computing area, he focused on estimating the circumference based on the sum of the perimeter edges of the polygons. Imagine iteratively doubling the sides of these polygons, slicing them into many tiny triangles, each subdividing the former and pushing closer to the circle’s edge. Using a theorem from Pythagoras, Archimedes was able to compute the length of the sides of these right triangles. As he progressed, dividing the former triangles into smaller ones, an ever more accurate estimation of the circumference emerged. He started with a hexagon, then doubled the sides four times to finish with a 96-sided polygon. Through this method, he narrowed down the value to between 3 10/71 and 3 1/7 (3.141 and 3.143).

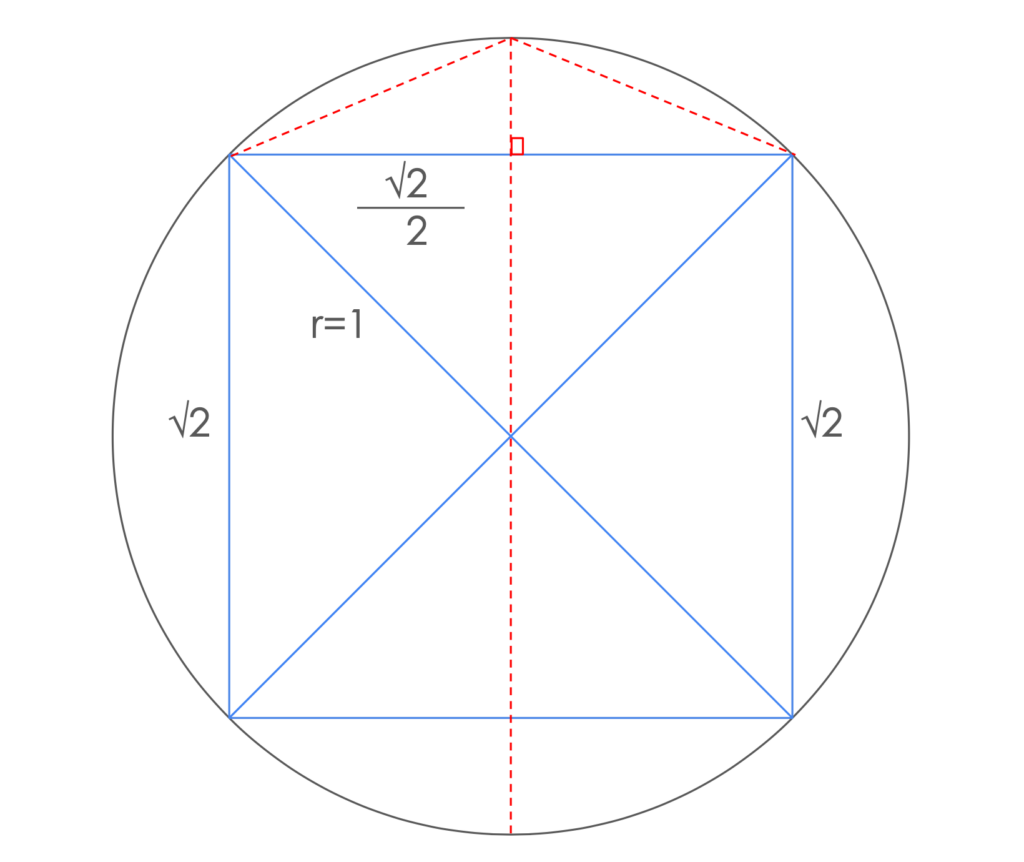
Using right triangle geometry and Pythagorean theorem, a2 + b2 = c2, you can compute the length of the edges to approximate the circumference of the circle.

Over the centuries, mathematicians across cultures and continents refined these approximations, each contributing a piece to the puzzle of this magical number. However, it wasn’t until the 17th century when mathematicians like Ludolph van Ceulen calculated this golden number to an unprecedented 35 decimal places. Humanity’s relentless pursuit of mathematical precision didn’t stop there. Our fascination with this mysterious golden ratio continued to motivate mathematicians, engineers, and enthusiasts alike. In 2022, researchers at Google announced computing it to 100 trillion decimal digits.  We still haven’t found the end. Its digits extend infinitely, never repeating in a discernible pattern, yet holding the key to understanding the fundamental property of circles. 

Of course, this fascinating ratio is the number we call Pi, represented by the Greek letter π. As we approach Archimedes estimate of 3.14 on our calendars as March 14, Pi Day, let’s celebrate the enduring curiosity and perseverance of our human family that led to the discovery of this remarkable number. It reminds us that even the most complex mysteries can be unraveled with dedication and ingenuity.

Here is a slice of Pi you can take with you this week. This simple python script will compute Pi to 100 places using Archimedes’ approach:

https://gist.github.com/jasonacox/dfc3f1c1d4e630009c80797352d81c32

Python
from decimal import Decimal, getcontext

def pi_archimedes(n):
    """
    Calculate Pi using Archimedes method with n iterations to estimate Pi.
    This method approximates Pi by calculating the perimeter of a polygon 
    inscribed within a unit circle.

    Polygon edge lengths are computed using the Pythagorean theorem and 
    the geometry of the polygons. The number of sides of the polygon is
    also doubled in each iteration, as each side of the polygon is 
    bisected to form a new polygon with twice as many sides.

    The formula is:
        sides = 2 * 2^n
        length^2 = 2 - 2 * sqrt(1 - length^2 / 4))

    After n iterations, the function returns the approximate value of 
    Pi using the formula:
        perimeter = sides * sqrt(length^2)
    """
    polygon_edge_length_sq = Decimal(2)
    polygon_sides = 2
    # Start with a line, then a square, then a octagon, etc.
    for _ in range(n):
        polygon_edge_length_sq = 2 - 2 * (1 - polygon_edge_length_sq / 4).sqrt()
        polygon_sides = polygon_sides * 2
    return polygon_sides * polygon_edge_length_sq.sqrt()

# Set the number of decimal places to calculate
PLACES = 100

# Calculate Pi with increasing iterations until the result converges at
# the desired number of decimal places
old_result = None
for n in range(10*PLACES):
    getcontext().prec = 2 * PLACES  # Do calculations with double precision
    result = pi_archimedes(n)
    getcontext().prec = PLACES      # Print the result with single precision
    result = +result                # Rounding
    print("%3d: %s" % (n, result))
    if result == old_result:        # Did it converge?
        break
    old_result = result

References